MHD Riemann Problems

I’ll be using a selection of MHD Riemann Problems and shock tubes to test my HLLD and overall MHD implementation so I wanted to gather some of the basics here. This post was originally written with information from Miniati & Martin 2011¹. Citations are at the bottom and images are cited in their captions.

Once MHD is fully implemented a followup post will follow with non-Riemann test problems such as the Orszag-Tang Vortex.

Table of Riemann Problems

Please note that many of the cited papers have typos in their initial conditions. These are the correct initial conditions as verified by the Athena code and the plots in the papers

Field	Brio & Wu2	Dai & Woodward3	Einfeldt Strong Rarefaction45	Ryu & Jones 1a6	Ryu & Jones 4d6
\( \gamma \)	\( 2 \)	\( \frac{5}{3} \)	\( 1.4 \)	\( \frac{5}{3} \)	\( \frac{5}{3} \)
\( t_{max} \)	\( 0.1 \)	\( 0.2 \)	\( 0.16 \)	\( 0.08 \)	\( 0.16 \)
Left
\( \rho \)	\( 1.0 \)	\( 1.08 \)	\( 1.0 \)	\( 1.0 \)	\( 1.0 \)
\( P \)	\( 1.0 \)	\( 0.95 \)	\( 0.45 \)	\( 20 \)	\( 1.0 \)
\( V_x \)	\( 0.0 \)	\( 1.2 \)	\( -v_0 = -2.0 \)	\( 10.0 \)	\( 0.0 \)
\( V_y \)	\( 0.0 \)	\( 0.01 \)	\( 0.0 \)	\( 0.0 \)	\( 0.0 \)
\( V_z \)	\( 0.0 \)	\( 0.5 \)	\( 0.0 \)	\( 0.0 \)	\( 0.0 \)
\( B_x \)	\( 0.75 \)	\( \frac{2}{\sqrt{4\pi}} \)	\( 0.0 \)	\( \frac{5}{\sqrt{4\pi}} \)	\( 0.7 \)
\( B_y \)	\( 1.0 \)	\( \frac{3.6}{\sqrt{4\pi}} \)	\( 0.5 \)	\( \frac{5}{\sqrt{4\pi}} \)	\( 0.0 \)
\( B_z \)	\( 0.0 \)	\( \frac{2}{\sqrt{4\pi}} \)	\( 0.0 \)	\( 0.0 \)	\( 0.0 \)
Right
\( \rho \)	\( 0.125 \)	\( 1.0 \)	\( 1.0 \)	\( 1.0 \)	\( 0.3 \)
\( P \)	\( 0.1 \)	\( 1.0 \)	\( 0.45 \)	\( 1.0 \)	\( 0.2 \)
\( V_x \)	\( 0.0 \)	\( 0.0 \)	\( v_0 = 2.0 \)	\( -10 \)	\( 0.0 \)
\( V_y \)	\( 0.0 \)	\( 0.0 \)	\( 0.0 \)	\( 0.0 \)	\( 0.0 \)
\( V_z \)	\( 0.0 \)	\( 0.0 \)	\( 0.0 \)	\( 0.0 \)	\( 1.0 \)
\( B_x \)	\( 0.75 \)	\( \frac{2}{\sqrt{4\pi}} \)	\( 0.0 \)	\( \frac{5}{\sqrt{4\pi}} \)	\( 0.7 \)
\( B_y \)	\( -1.0 \)	\( \frac{4}{\sqrt{4\pi}} \)	\( 0.5 \)	\( \frac{5}{\sqrt{4\pi}} \)	\( 1.0 \)
\( B_z \)	\( 0.0 \)	\( \frac{2}{\sqrt{4\pi}} \)	\( 0.0 \)	\( 0.0 \)	\( 0.0 \)

Details on Each Problem

Brio & Wu Shock Tube²

The Brio & Wu Shock Tube is essentially a Sod Sock Tube with magnetic fields. It shows most of the MHD waves and is a good stress test for approximate Riemann solvers and MHD simulation code.

Waves, left to right:

1. Fast rarefaction
2. Compound wave
3. Contact discontinuity
4. Slow shock
5. Fast rarefaction

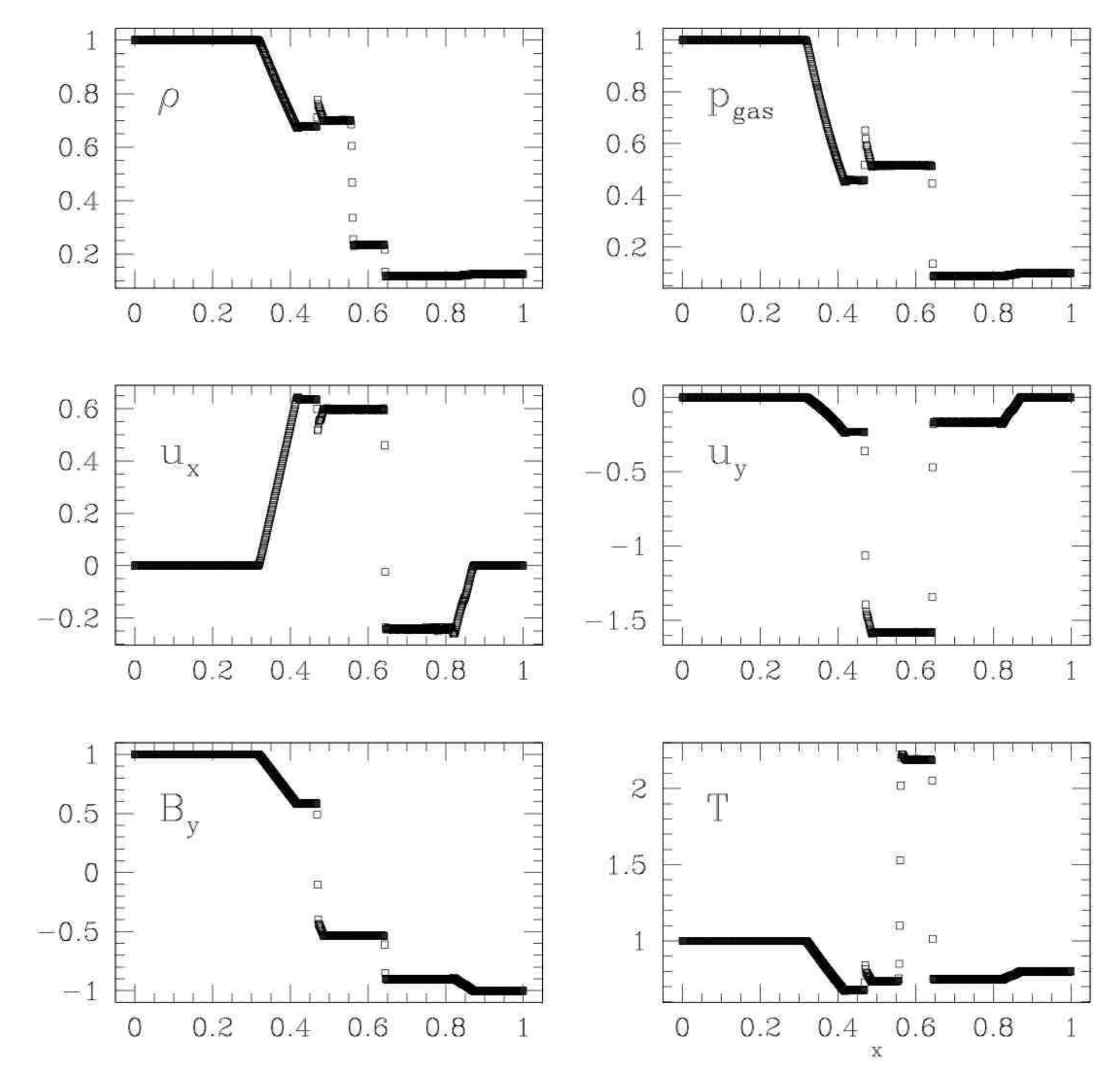Brio & Wu Shock Tube at \( t=0.1 \). Source: Figure 2 from Miniati & Martin 2011¹

Dai & Woodward Shock Tube³

The Dai & Woodward Shock Tube produces 3 pairs of MHD waves moving outwards from the central contact discontinuity. This is probably a more robust test of MHD than the Brio & Wu Shock Tube since it shows all 7 MHD waves.

Waves, left ot right:

1. Fast shock
2. Alfvên/Rotation waves
3. Slow shock
4. Contact discontinuity
5. Slow shock
6. Alfvên/Rotation waves
7. Fast shock

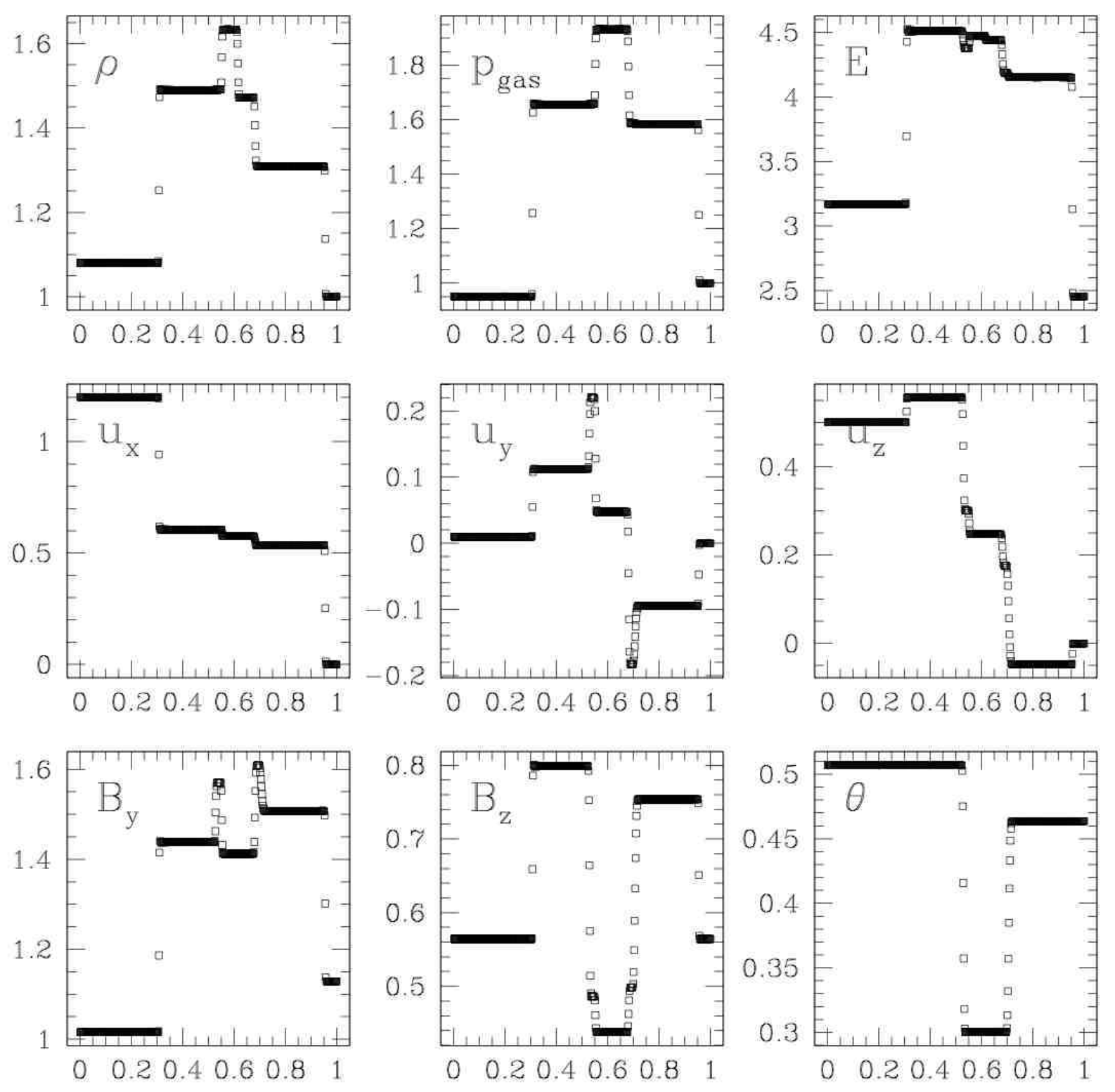Dai & Woodward Shock Tube at \( t=0.2 \). Source: Figure 3 from Miniati & Martin 2011¹

Einfeldt Strong Rarefaction⁴⁵

This is the only test here that isn’t a shock tube. We have identical initial conditions on both sides, except the \( x \)-velocity which is negative on the left side and positive on the right. This velocity, \( V_0 \), can lead to spurious oscillation with high order Godunov schemes¹ when \( V_0 \) is large (\( V_0 \ge 3 \)) and so I’ve chosen a more conservative value of \( V_0=2 \) . These diverging fluids lead to an extremely strong and fast rarefaction where the energy is dominated by kinetic energy and can often reveal issues in code accuracy since it can lead to nonphysical states with negative density or internal energy

Waves, left ot right:

1. Fast rarefaction
2. Fast rarefaction

EinFeldt Strong Rarefaction at \( t=0.16 \). Source: Figure 5 from Miniati & Martin 2011¹

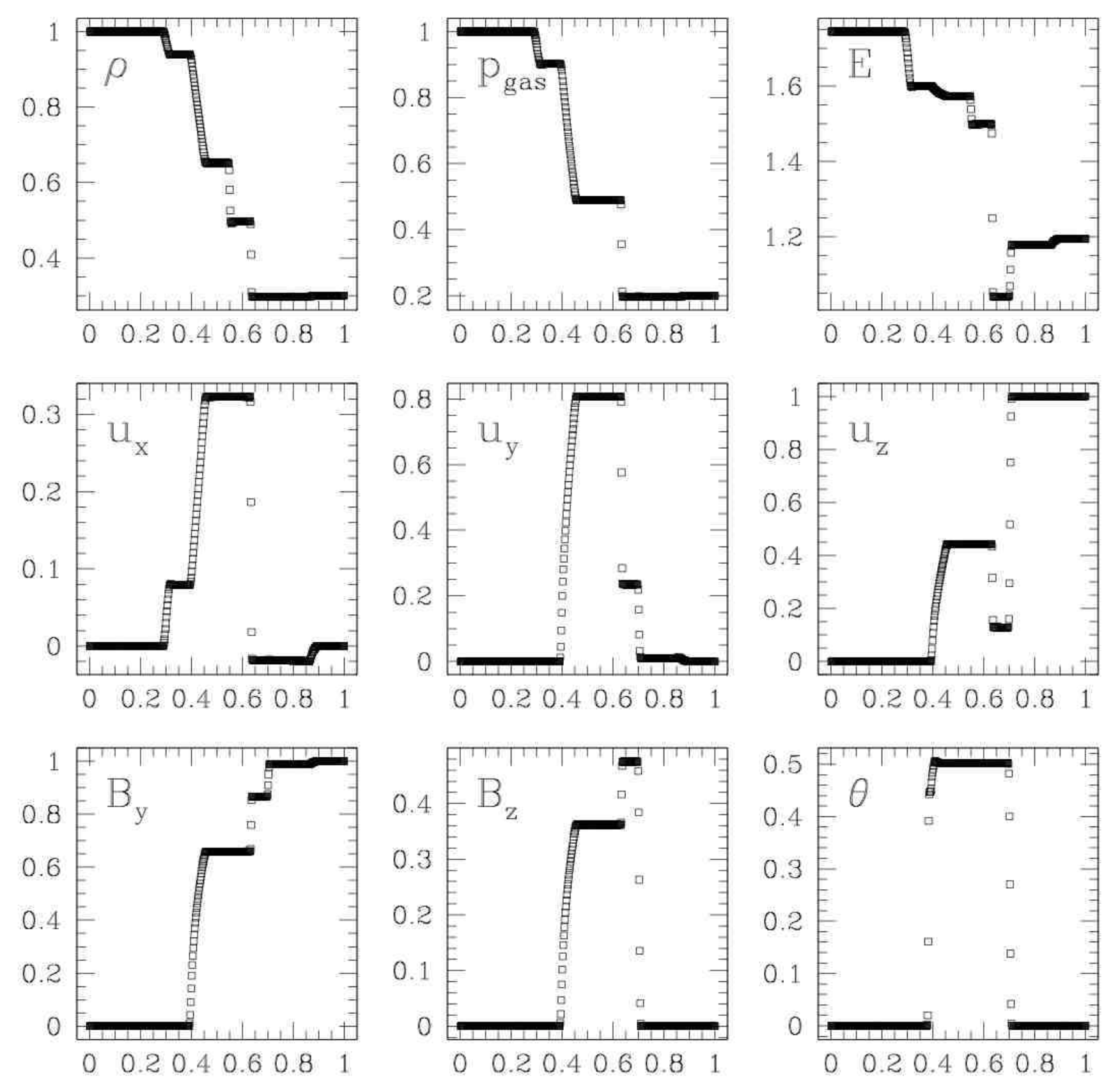
Ryu & Jones Shock Tube 1a⁶

Ryu & Jones 1995 contains a wealth of different shock tubes and is an excellent resource. Shock tube 1a has a fairly simple and easy to read set of 5 waves. Does not include an Alfvên wave

Waves, left ot right:

1. Fast shock
2. Slow rarefaction
3. Contact discontinuity
4. Slow shock
5. Fast shock

Ryu & Jones Shock Tube at \( t=0.08 \). Source: Figure 1a from Ryu & Jones 1995 ⁶

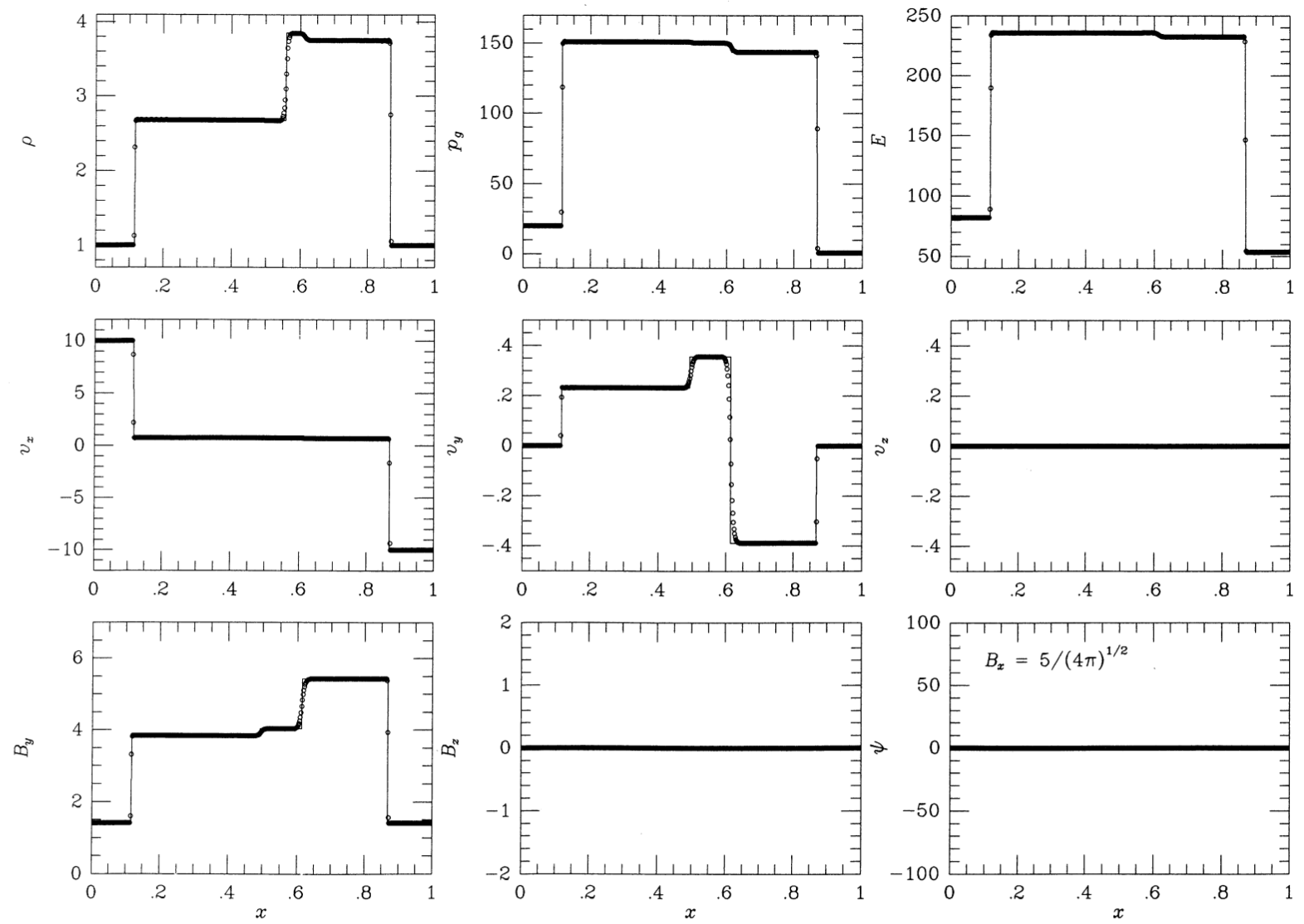
Ryu & Jones Shock Tube 4d⁶

Shock Tube 4d features a switch-on slow rarefaction. Switch-on/off magnetosonic waves cause the tangential magnetic field to turn on/off.

Waves, left ot right:

1. Hydrodynamic rarefaction
2. Switch on slow shock
3. Contact discontinuity
4. Slow Shock
5. Alfvên/Rotation wave
6. Fast rarefaction

Ryu & Jones Shock Tube at \( t=0.16 \). Source: Figure 4 from Miniati & Martin 2011¹

Citations

1. Miniati, F., & Martin, D. F. (2011). Constrained-transport magnetohydrodynamics with adaptive mesh refinement in CHARM. Astrophysical Journal, Supplement Series, 195(1). https://doi.org/10.1088/0067-0049/195/1/5 ↩︎ ↩︎² ↩︎³ ↩︎⁴ ↩︎⁵ ↩︎⁶

2. Brio, M., & Wu, C. C. (1988). An Upwind Differencing Scheme for the Equations of Ideal Magnetohydrodynamics. JOURNAL OF COMPUTATIONAL PHYSICS, 75, 40–422. https://ui.adsabs.harvard.edu/abs/1988JCoPh..75..400B/abstract ↩︎ ↩︎²

3. Dai, W., & Woodward, P. R. (1998). ON THE DIVERGENCE-FREE CONDITION AND CONSERVATION LAWS IN NUMERICAL SIMULATIONS FOR SUPERSONIC MAGNETOHYDRODYNAMIC FLOWS. THE ASTROPHYSICAL JOURNAL, 494, 317–335. https://iopscience.iop.org/article/10.1086/305176/meta ↩︎ ↩︎²

4. Einfeldt, B., Munz, C. D., Roe, P. L., & W green, B. (1991). On Godunov-Type Methods near Low Densities. JOURNAL OF COMPUTATIONAL PHYSICS, 92, 213–295. https://ui.adsabs.harvard.edu/abs/1991JCoPh..92..273E/abstract ↩︎ ↩︎²

5. Miyoshi, T., & Kusano, K. (2005). A multi-state HLL approximate Riemann solver for ideal magnetohydrodynamics. Journal of Computational Physics, 208(1), 315–344. https://doi.org/10.1016/j.jcp.2005.02.017 ↩︎ ↩︎²

6. Ryu, D., Jones, T. W., & Frank, A. (1995). Numerical Magnetohydrodynamics in Astrophysics: Algorithm and Tests for Multi-Dimensional Flow 1. The Astrophysical Journal. https://ui.adsabs.harvard.edu/abs/1995ApJ…442..228R/abstract ↩︎ ↩︎² ↩︎³ ↩︎⁴ ↩︎⁵